[TIL] Tree
트리 자료 구조는 자식 노드를 지닌 노드들로 구성된다. 일반적으로 DOM Tree에서 확인한 모양으로 가장 최상위에 root node를 갖고 있고 자식들이 아래로 마치 가지치기한 형태의 뻗어있다.
차근차근 다양한 Tree 구조에 대해 정리해보겠다.
일반 Tree 구조
일반적인 트리 구조는 많은 자식들을 갖고 있을 수 있다. 일반적으로 아래와 같이 간단하게 코드를 구현한다.
function TreeNode(value) {
this.value = value;
this.children = [];
}TreeNode로 인스턴스를 만들면서 값을 넣어주고 자식들은 children에 넣어주면 된다.
이진트리 (Binary Tree)
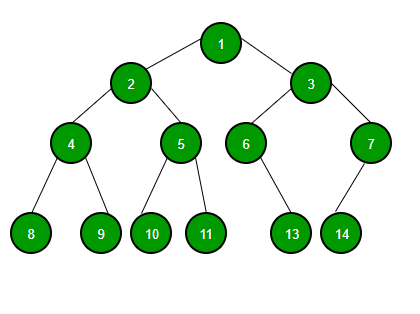출처: Geeks for Geeks
이진트리는 자식 노드가 왼쪽, 오른쪽인 최대 두 개뿐인 트리구조이다.
이진트리도 종류에 따라 완전이진트리, 포화이진트리, 균형이진트리, 편향이진트리 등이 있지만, 나머지는 추후 따로 정리해보도록 하겠다.
이진트리를 구현하기 위해서는 먼저 이진트리를 구성하는 node가 필요할 것이다. 아래와 같이 생성자 함수 코드로 작성할 수 있다. 이 함수를 잘 기억해둬야 추후 순회 알고리즘을 이해할 수 있다. node의 left와 right를 갖고 있는 점을 기억해두자.
function BinaryTreeNode(value) {
this.value = value;
this.left = null;
this.right = null;
}노드를 만들었으면 이제 트리에 추가하기 위한 객체를 만들자. node를 만들었던 방식으로 생성자 함수를 사용해 BinaryTree 함수를 만든다. 이 BinaryTree 함수에는 root값이 null인 프로퍼티를 초기 값으로 설정한다. 이후 위의 node를 생성하면서 root에 추가하고 왼쪽과 오른쪽에 node 객체를 재할당 하는 방식으로 진행한다.
function BinaryTree() {
this._root = null;
}트리순회(Tree Traversal)
트리의 경우 트리의 모든 항목을 방문하기 위해 왼쪽 포인터와 오른쪽 포인터가 존재한다고 한다. 그리고 순회 방법에는 선순위(pre-order), 후순위(post-order), 중순위(in-order), 단계순위(level-order) 순회가 있다. 이 방법 또한 차근차근 정리해 보겠다.
# 선순위순회 (Pre-order Traversal)
출처: Techie Delight
선순위 순회는 루트노드에서 시작해 왼쪽노드부터 차례대로 다 순회한 후 오른쪽노드 순으로 순회한다. 처음에는 코드로 이해하기 힘들었지만, 원리를 파악하면서 느낀 부분은 순회 순서와 코드 순서를 잘 이해하는 것이 코드 이해의 핵심이었다. 재귀함수의 경험이 없다보니 재귀함수를 작성하거나 이해할 때 이해의 핵심포인트를 찾으려고 노력한다.
BinaryTree.prototype.traversePreOrder = funciton() {
traversePreOrderHelper(this._root); // 가장 최상위인 root node를 전달해 실행
function TraversePreOrderHelper(node) {
if(!node) return; // (1) 인자로 받은 노드가 없을 때, 즉시 함수 종료
console.log(node.value) // (2) 인자로 받은 노드가 있으니 값을 출력
traversePreOrderHelper(node.left); // (3) 왼쪽부터 순회해야하기 때문에
// 재귀함수를 통해 모든 left
// node부터 인자로 전달
// 조건문으로 left가 있는지 확인을 먼저
// 하는 것이 아닌 것이 바로 left를 넣어
// 실행하는 것이 이해의 핵심이었다.
traversePreOrderHelper(node.right); // (4) 왼쪽이 끝났으면 오른쪽 node
// 를 모두 순회
}
}TL;DR: 위의 코드 동작
위의 코드를 통해 그림을 설명해보자면, 간단하게 표현한 1의 값을 갖고있는 root node node: 1을
traversePreOrderHelper(this._root)함수의 인자로 전달해 함수를 실행한다.- 함수의 (1)번 부분에서 node가 null이 아니니 바로 (2)번이 실행되어 값이 출력된다.
- 그리고 (3)번 부분에서 root node의 left인
node: 2가 인자로 넘어가traversePreOrderHelper(node:2)가 실행된다. traversePreOrderHelper재귀적으로 실행되어 다시 (1), (2)번을 거쳐 (3)번 실행지점으로 도착하고 left에node: 4가 인자로 넘어가traversePreOrderHelper(node:4)함수가 실행된다.- 다시 재귀 함수를 통해 (1), (2)번을 거쳐 (3)번에서 함수를 실행하려 하지만 다음 left 노드가 null이기 때문에
traversePreOrderHelper(null)이 실행 - 다음 함수 실행 이후 node가 없으므로 (1)번 부분에서 즉시 종료되고 (4)번이 실행되는데 right node 또한 null이기 때문에
traversePreOrderHelper(null)실행되고 반복된다. traversePreOrderHelper(node: 4)의 실행은 완전 종료되고traversePreOrderHelper(node:2)의 내부로 돌아와 (4)번이 실행되지만 right node가 null이므로 역시 즉시 종료되며 함수traversePreOrderHelper(node: 2)의 실행도 종료된다.traversePreOrderHelper(this._root)의 내부로 돌아와 right node가 (4)번 함수 인자로 넘어가traversePreOrderHelper(node: 3)이 실행된다.- 과정이 반복된다.
좀 장황하고 길지만 쉬운 이해를 위해 풀어 정리했다.
# 중순위순회 (Pre-order Traversal)
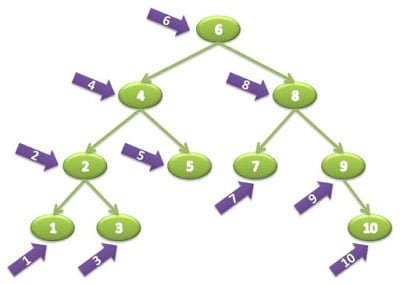출처: DEV 블로그
중순위순회는 가장 왼쪽 노드, 현재노드(루트노드), 오른쪽 노드 순으로 순회한다. 위의 그림을 보면 이해가 더 빠르다. 이 중순위 또한 재귀 함수로 구현하는 것이 쉽다고 한다.
코드에서 이해의 핵심 부분은 순회 순서가 가장 왼쪽부터라 할 지라도 코드에서 접근하는 첫 번째 노드는 root node이며, root node에서 가장 왼쪽을 먼저 찾아가는 것이 중요하다고 느꼈다.
위의 선순위 순회에서 설명한 내용을 통해 기본적인 가닥은 이해될 것이라고 생각하여 선순위 순회의 설명보다는 간략하게 정리하겠다.
BinaryTree.prototype.traverseInOrder = function() {
travseInOrderHelper(this._root); // root 부터 시작
function travserInOrderHelper(node) {
if(!node) return; //(1) node가 없으면? 함수 즉시 종료
travseInOrderHelper(node.left); // (2) left 노드를 넣어 주고 함수를 재귀적 실행하면
// console이 이 함수 다음에 실행되므로 가장 왼쪽
// node를 먼저 찾아간다.
console.log(node.value); // (3) 값이 출력된다.
travserInOrderHelper(node.right); // (4) right node를 넣어 재귀적 실행하면 다시
// right node의 left가장 왼쪽을 찾아 들어간다.
}
}위의 함수는 console.log 메서드 left node를 실행하는 함수 다음에 실행되는 것이 핵심 포인트라고 생각한다. 간략하게 설명하자면,
- root 부터
travserInOrderHelper(root)함수를 실행한다. - left node가 있으므로 (2)번의
travserInOrderHelper(node: 4)실행된다. 다시 재귀 실행으로travserInOrderHelper(node: 1)까지 실행된다. travserInOrderHelper(node: 1)의 left node는 null이기 때문에, 실행이 종료되고 (3)번이 실행되어 1이 출력된다.travserInOrderHelper(node: 1)의 right node가 null이므로 함수는 종료된다.- 생략되었던
travserInOrderHelper(node: 2)내부의 (2)번에서 실행된 함수인travserInOrderHelper(node: 1)이 종료되었기 때문에 (3)번 console.log가 실행되어 2가 출력된다. - (4)번이 실행되어
travserInOrderHelper(node: 3)이 실행되고,node: 3의 left right가 없으므로 3이란 값이 출력되고 종료된다. travserInOrderHelper(node: 2)가 완전히 종료되고travserInOrderHelper(node: 4)의 (2)번이 끝나 (3)번이 실행되어 4란 값이 출력된다.- (4)번이 실행되며 이후 앞의 과정이 반복된다.
# 후순위순회 (Post-order Traversal)
출처: Techie Delight
후순위 순회는 가장 왼쪽 끝의 노드부터 오른쪽, 현재노드(루트노드) 순으로 마지막 부분을 먼저 순회하는 것이다. 위의 그림의 아랫부분 설명을 보면 이해가 쉽다. root 노드가 가장 마지막에 출력된다고 이해하면 된다.
후순위 순회의 코드는 if 조건문을 통해 재귀함수를 호출했다. 그리고 node의 left와 right를 모두 체크한 후 console.log를 실행해 값을 출력했다. 이를 통해 느낀점은 왼쪽으로 찾아가서 순회하는 다른 코드와 다르게 가장 마지막 순서를 찾기 위해 체크를 하고 접근하는 방식이 핵심이라고 생각했다. 언제든지 오른쪽의 depth에도 접근할 수 있는 것처럼 말이다.
코드를 보자면 아래와 같다.
BinaryTree.prototype.travserPostOrder = function() {
traversePostOrderHelper(this._root);
function travserPostOrderHelper(node) {
if(node.left) { // 이 것도 어쨌든 방향은 왼쪽에서 오른쪽이기 때문에
// left node 부터 체크
traversePostOrderHelper(node.left); // 재귀를 통해 left가 있다면 일단
// 가장 왼쪽으로 찾아 간다.
}
if(node.right) {
traversePostOrderHelper(node.left); // left가 없으면 right를 찾는다. right의
// depth가 길다면, left의 depth는 없다면,
// right를 계속 찾아간다.
}
console.log(node.value); // left와 right node 모두 없다면 출력된다. 더 이상 검색
// 할 depth가 없으므로.
}
}선순위 중순위의 설명 덕분에 이제는 이해가 수월할테니 자세한 설명은 생략하도록 하겠다.
# 단계순위순회 (BFS: Breadth First Search)
출처: Algorithms
처음 공부할때 너무 어려웠던 개념의 BFS, 단계순위순회 방식이다. 말그대로 root부터 시작해 왼쪽부터 오른쪽으로 순회하면서 차례대로 한 줄씩 내려가는 순회방식이다. 위의 그림에서는 1부터 차례대로 숫자를 순회한다고 보면 된다. (1, 2, 3, 4 …)
사실 개념이 어려웠다기 보다는 코드로 구현하는 것이 어려웠다. 처음에 Stack과 Queue의 개념을 배우면서 BFS, DFS 방식을 통한 Parser를 구현한 적이 있었는데 정확하게 이해하지 못하고 찾아가며 구현했던 터라 언제든지 복습하고 또 복습할 예정이였다. 오늘이 그 복습날들 중 하나인 셈이다.
이해의 핵심은 queue에 left와 right를 저장하고 반복문을 통해 다시 queue에 저장했던 node들을 선입선출 방식으로 접근해 queue에 다음 노드들을 차례대로 저장하며 하나씩 순회하는 방법이다. 추후 코드와 함께 순서를 정리하겠다.
BinaryTree.prototype.travserLevelOrder = function() {
//너비 우선 검색
let root = this._root; // (1)
const queue = []; // (2)
if(!root) return; // (3)
queue.push(root); // (4)
while(queue.length) { // (5)
const temp = queue.shift(); // (6)
console.log(temp.value); // (7)
if(temp.left) queue.push(temp.left); // (8)
if(temp.right) queue.push(temp.right); // (9)
}
}- (1) 먼저 root 변수에 this.root를 할당하여 생성한다. (불필요한 추가 작업일 수도 있기에 직접 this.root를 넣어도 될 것 같다.) 그리고 (2) queue라는 배열을 하나 선언한다.
- (3) 마찬가지로 root의 값이 null이라면? 즉시 종료한다.
- (4) root에 노드가 있으니 이를 queue에 저장한다. (현재: [root])
- (5) 반복문의 종료 조건은 queue가 비어진 상태일 때이다. queue가 빈 상태가 되면 모든 node를 다 순회했다는 의미가 될 것이다.
- (6) root를 queue에서 빼 temp에 저장한 후 (7) 값을 console로 출력한다.
- (8) left가 있으니 left를 queue에 저장한다. (현재: [node:2])
- (9) right가 있으니 right를 queue에 저장한다. (현재: [node:2, node:3])
- (5) queue에 데이터가 있으니 반복문이 실행되고 (6)
node:2를 temp에 저장하고 (7) console로 출력한다. (현재: [node:3]) - (8) (9) left와 right가 있으니 queue에 모두 저장한다. (현재: [node:3, node:4, node:5])
- (5) queue에 데이터가 있으니 반복문이 실행되고 (6)
node:3를 temp에 저장하고 (7) console로 출력한다. (현재: [node:4, node:5]) -
- (8) (9) left와 right가 있으니 queue에 모두 저장한다. (현재: [node:4, node:5, node:6, node:7])
- 이후 반복된다.
차근차근 이해하니 다른 순회보다 더 쉬운 것 같다. 재귀함수를 사용하는 것 보다 반복문을 사용하는 것이 쉽기 때문에 이 코드를 많이 사용하는 것으로 알고 있어 더 이해가 쉬운 것 같다.
정리가 많이 길어졌기 때문에 Binary Search Tree에 대해서는 2편에서 정리해야하겠다. 자료구조는 공부할 수록 어렵긴 하지만, 이런 규칙을 찾아낸 사람들이 대단하다고 느낀다. 공부할 수록 재밌는 분야라고 생각된다. 기본기를 쌓기 위해서라도 꾸준히 정리할 예정이다.
도움받은 문서
공부한 내용을 정리하는 공간으로 학습 중 습득한 내용이 정확하지 않은 정보를 포함할 수 있어 추후 발견시 수정하도록 하겠습니다.